Skip to main content

搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。 每列的元素从上到下升序排列。

示例 1：

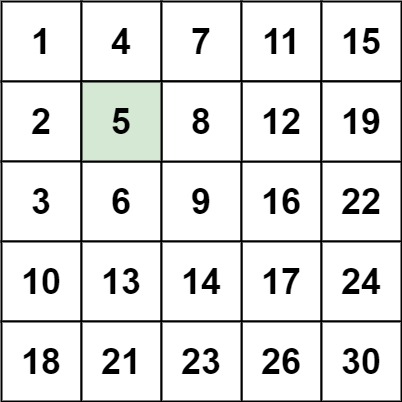image 输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出：true 示例 2：

image 输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出：false

简单做法：一层一层确定边界，比目标值大则为边界，横纵缩小边界范围，再开始下一层边界查找，缩小边界，直到找到为止(和进阶做法一致)。

进阶做法： 要在每行、每列均升序排列的m×n矩阵中高效搜索目标值，可以利用矩阵的单调性，从右上角（或左下角）开始搜索，通过逐步缩小范围实现O(m + n)时间复杂度的解法。

核心思路​

矩阵的特性：

  • 每行从左到右递增（同一行中，左边元素 < 右边元素）；
  • 每列从上到下递增（同一列中，上边元素 < 下边元素）。

选择右上角元素作为起始点（记为 matrix[i][j]），其特点是：

  • 它是当前行的最大值（比同行左侧所有元素大）；
  • 它是当前列的最小值（比同列下方所有元素小）。

通过与目标值 target 比较，可快速缩小搜索范围：

  • 若 matrix[i][j] == target：找到目标，返回 true；
  • 若 matrix[i][j] > target：目标不可能在当前列（列中下方元素更大），则左移一列（j--）；
  • 若 matrix[i][j] < target：目标不可能在当前行（行中左侧元素更小），则下移一行（i++）。

重复上述步骤，直到找到目标或指针超出矩阵范围（此时返回 false）。

代码实现​

function searchMatrix(matrix, target) {
    if (matrix.length === 0) return false; // 矩阵为空
    
    let m = matrix.length;    // 行数
    let n = matrix[0].length; // 列数
    let i = 0;                // 起始行（第一行）
    let j = n - 1;            // 起始列（最后一列，右上角）
    
    while (i < m && j >= 0) {
        const current = matrix[i][j];
        if (current === target) {
            return true; // 找到目标
        } else if (current > target) {
            j--; // 目标在左侧，左移一列
        } else {
            i++; // 目标在下方，下移一行
        }
    }
    
    return false; // 遍历完未找到目标
}

示例分析​

以矩阵 matrix = [[1,4,7,11],[2,5,8,12],[3,6,9,16],[10,13,14,17]]，目标 target = 5 为例：

  1. 起始位置：i=0, j=3（元素 11）。
    • 11 > 5 → 左移一列（j=2，元素 7）。
  2. 当前元素 7 > 5 → 左移一列（j=1，元素 4）。
  3. 当前元素 4 < 5 → 下移一行（i=1，元素 5）。
  4. 5 == 5 → 找到目标，返回 true。

与其他方法的对比​

方法时间复杂度空间复杂度特点
暴力搜索O(mn)O(1)遍历所有元素，效率低
逐行二分O(m log n)O(1)每行二分查找，优于暴力
右上角搜索O(m + n)O(1)最优解，利用单调性快速缩范围

边界情况验证​

  • 矩阵为空（m=0 或 n=0）：返回 false。
  • 目标小于矩阵最小值（如 target < matrix[0][0]）：返回 false。
  • 目标大于矩阵最大值（如 target > matrix[m-1][n-1]）：返回 false。
  • 目标在第一行或最后一列：能被正确搜索到。

总结​

该方法的核心是利用矩阵的单调性选择合适的起始点（右上角或左下角），通过比较目标值与当前元素，逐步排除整行或整列，将搜索范围从“m×n”缩小到“0”，最终实现O(m + n)的高效搜索。这种思路无需额外空间，且逻辑直观，是解决此类矩阵搜索问题的最优解。