Skip to main content

矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

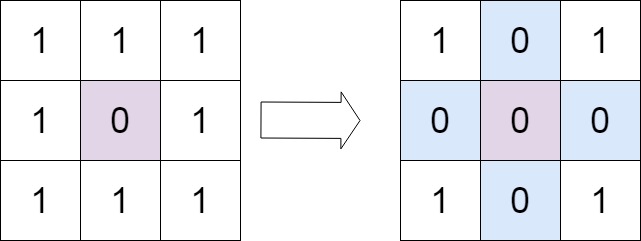
示例 1： image

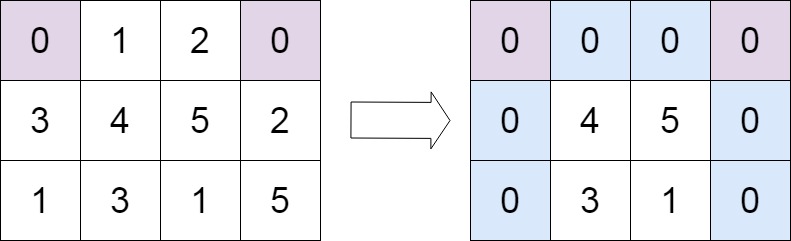
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出：[[1,0,1],[0,0,0],[1,0,1]] 示例 2： image

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

简单做法：先获取几行几列，再遍历所有0的坐标，再将对应坐标的行和列都设置为0

进阶做法：原地算法

方法思路​

  1. 标记首行和首列：检查矩阵的第一行和第一列是否原本存在 0，用布尔变量记录。
  2. 利用首行首列标记：遍历矩阵其余元素，若 matrix[i][j] == 0，则将 matrix[i][0] 和 matrix[0][j] 置为 0，利用首行首列作为标记数组。
  3. 根据标记置零：遍历首行首列以外的元素，若 matrix[i][0] == 0 或 matrix[0][j] == 0，则将 matrix[i][j] 置为 0。
  4. 处理首行首列：根据步骤 1 的标记，决定是否将首行或首列全部置零。

代码实现​

function setZeroes(matrix) {
    const m = matrix.length;
    if (m === 0) return;
    const n = matrix[0].length;
    
    // 标记首行和首列是否原本存在 0
    let firstRowHasZero = false;
    let firstColHasZero = false;
    
    // 检查首行
    for (let j = 0; j < n; j++) {
        if (matrix[0][j] === 0) {
            firstRowHasZero = true;
            break;
        }
    }
    
    // 检查首列
    for (let i = 0; i < m; i++) {
        if (matrix[i][0] === 0) {
            firstColHasZero = true;
            break;
        }
    }
    
    // 利用首行首列标记其余行和列
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            if (matrix[i][j] === 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }
    
    // 根据标记置零（不处理首行首列）
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            if (matrix[i][0] === 0 || matrix[0][j] === 0) {
                matrix[i][j] = 0;
            }
        }
    }
    
    // 处理首行
    if (firstRowHasZero) {
        for (let j = 0; j < n; j++) {
            matrix[0][j] = 0;
        }
    }
    
    // 处理首列
    if (firstColHasZero) {
        for (let i = 0; i < m; i++) {
            matrix[i][0] = 0;
        }
    }
}

复杂度分析​

  • 时间复杂度：O(m×n)，需遍历矩阵三次。
  • 空间复杂度：O(1)，仅使用常数级额外空间。

示例分析​

输入矩阵：

[
  [1, 1, 1],
  [1, 0, 1],
  [1, 1, 1]
]
  1. 标记首行首列：首行和首列均无 0，标记为 false。
  2. 利用首行首列标记：发现 matrix[1][1] == 0，将 matrix[1][0] 和 matrix[0][1] 置为 0： 
    [
      [1, 0, 1],
      [0, 0, 1],
      [1, 1, 1]
    ]
  3. 根据标记置零：将 matrix[1][0] == 0 和 matrix[0][1] == 0 对应的元素置零： 
    [
      [1, 0, 1],
      [0, 0, 0],
      [1, 0, 1]
    ]
  4. 处理首行首列：首行首列无需置零，最终结果： 
    [
      [1, 0, 1],
      [0, 0, 0],
      [1, 0, 1]
    ]

正确性验证​

  • 覆盖所有情况：通过首行首列的标记，确保所有原 0 所在的行列被正确置零。
  • 避免误操作：先检查首行首列是否原本存在 0，避免因后续标记导致误判。

此方法通过巧妙利用矩阵自身的首行首列作为标记数组，在不使用额外空间的情况下完成任务，是最优解。