Skip to main content

相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

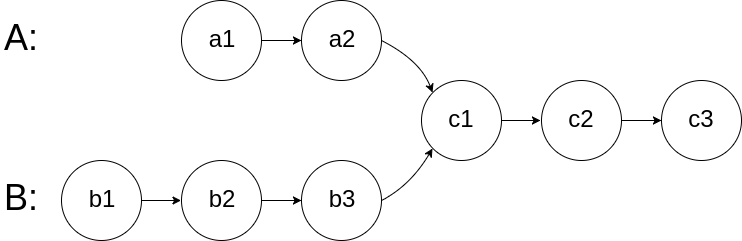
image

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0 listA - 第一个链表 listB - 第二个链表 skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数 skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数 评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

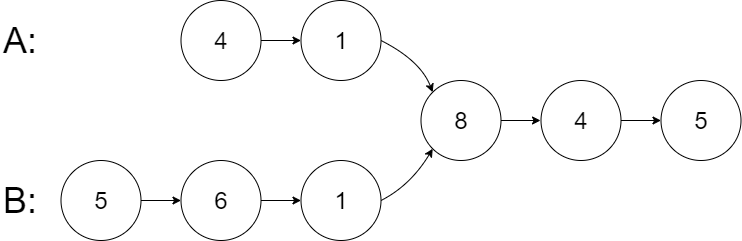
image

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出：Intersected at '8' 解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。 在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。 — 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

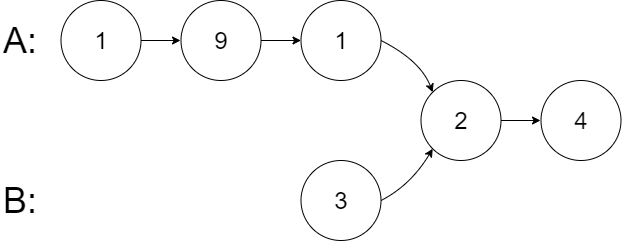
image

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出：Intersected at '2' 解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。 在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。 示例 3：

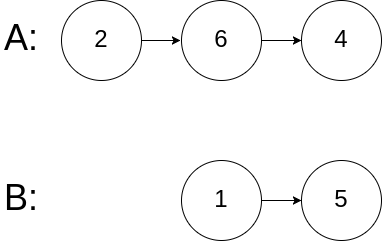
image

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出：No intersection 解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。 由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。 这两个链表不相交，因此返回 null 。

逻辑很简单，但是看不懂题目 做法：要找到两个单链表的相交节点，可以通过以下高效方法实现：

方法思路​

  1. 计算链表长度：分别遍历两个链表，得到它们的长度 lenA 和 lenB。
  2. 对齐起点：让较长的链表指针先走 |lenA - lenB| 步，使两个指针到相交点的剩余距离相等。
  3. 同步遍历：两个指针同时前进，若相遇则为相交节点；若均到达末尾（null），则无相交。

代码实现​

function getIntersectionNode(headA, headB) {
    // 计算链表A的长度
    let lenA = 0;
    let currA = headA;
    while (currA) {
        lenA++;
        currA = currA.next;
    }
    
    // 计算链表B的长度
    let lenB = 0;
    let currB = headB;
    while (currB) {
        lenB++;
        currB = currB.next;
    }
    
    // 重置指针
    currA = headA;
    currB = headB;
    
    // 让较长的链表指针先走 |lenA - lenB| 步
    if (lenA > lenB) {
        for (let i = 0; i < lenA - lenB; i++) {
            currA = currA.next;
        }
    } else {
        for (let i = 0; i < lenB - lenA; i++) {
            currB = currB.next;
        }
    }
    
    // 同步遍历找相交点
    while (currA !== currB) {
        currA = currA.next;
        currB = currB.next;
    }
    
    return currA; // 相交点或null
}

复杂度分析​

  • 时间复杂度：O(m + n)，其中 m 和 n 分别为两个链表的长度。
  • 空间复杂度：O(1)，仅需常数级额外空间。

示例验证​

  • 相交情况：
    链表A：1 → 2 → 3 → 6 → 7
    链表B：4 → 5 → 6 → 7

    • 计算长度：lenA = 5，lenB = 4。
    • 对齐起点：A先走 5 - 4 = 1 步，指向节点 2。
    • 同步遍历：A从 2、B从 4 开始，最终在节点 6 相遇，返回 6。

  • 不相交情况：
    链表A：1 → 2 → 3
    链表B：4 → 5 → 6

    • 计算长度：lenA = 3，lenB = 3。
    • 对齐起点：无需移动。
    • 同步遍历：A和B均到达 null，返回 null。

正确性证明​

  • 若链表相交，对齐起点后，两个指针到相交点的距离相等，同步遍历必然在相交点相遇。
  • 若链表不相交，同步遍历会同时到达末尾（null），返回 null。

该方法通过预处理长度差，确保指针同步移动时能正确相遇，是解决此类问题的最优解。