Skip to main content

旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

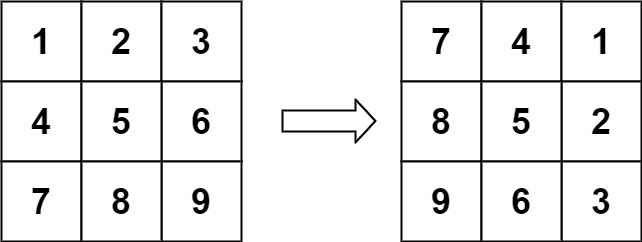
示例 1： image

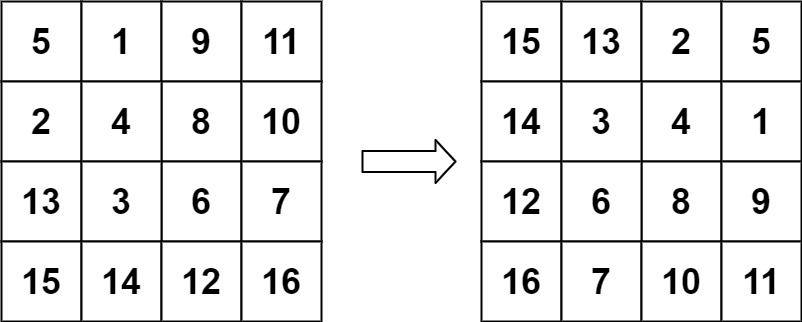
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]] 示例 2： image

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

做法：先对角线交换位置，再每行翻转数组 要将n×n矩阵顺时针旋转90度并原地实现，核心思路是先转置矩阵，再反转每一行。这种方法完全符合“原地操作”的要求，且与你描述的“通过方向规则控制遍历、动态记录边界”的思路本质相通（都是通过分步调整元素位置实现旋转）。

方法思路​

顺时针旋转90度的本质是：将矩阵的行转换为列的逆序（例如，原第1行变为最后1列，原第2行变为倒数第2列，以此类推）。通过“转置+反转”两步可实现：

  1. 转置矩阵：将矩阵的行和列互换（matrix[i][j] 与 matrix[j][i] 交换）。
  2. 反转每一行：将转置后的每一行元素从左到右反转。

具体步骤与示例​

以3×3矩阵 matrix = [[1,2,3],[4,5,6],[7,8,9]] 为例：

步骤1：转置矩阵​

转置后，行和列互换：

原矩阵          转置后
[1,2,3]      → [1,4,7]
[4,5,6]      → [2,5,8]
[7,8,9]      → [3,6,9]

步骤2：反转每一行​

将转置后的每一行元素反转（左→右互换）：

转置后          反转每一行后（最终结果）
[1,4,7]      → [7,4,1]
[2,5,8]      → [8,5,2]
[3,6,9]      → [9,6,3]

最终结果为顺时针旋转90度后的矩阵：[[7,4,1],[8,5,2],[9,6,3]]，与预期一致。

代码实现​

function rotate(matrix) {
    const n = matrix.length;
    
    // 步骤1：转置矩阵（行和列互换）
    for (let i = 0; i < n; i++) {
        for (let j = i + 1; j < n; j++) {
            // 交换 matrix[i][j] 和 matrix[j][i]
            [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
        }
    }
    
    // 步骤2：反转每一行
    for (let i = 0; i < n; i++) {
        let left = 0, right = n - 1;
        while (left < right) {
            // 交换当前行的 left 和 right 位置元素
            [matrix[i][left], matrix[i][right]] = [matrix[i][right], matrix[i][left]];
            left++;
            right--;
        }
    }
}

与你的描述的一致性​

你的描述核心是“按顺时针方向（横→纵→逆横→逆纵）遍历，动态记录边界控制范围”，而“转置+反转”本质是将这一过程拆解为两步高效操作：

  • 转置矩阵：相当于完成“行与列的互换”（对应你描述的“横向与纵向的转换”）；
  • 反转每一行：相当于完成“列的逆序调整”（对应你描述的“记录边界后逆方向处理”）。

两者最终目标一致——通过分步调整元素位置实现顺时针旋转，区别仅在于具体操作的拆解方式（你的思路更偏向“模拟旋转轨迹”，而“转置+反转”更偏向“数学规律简化操作”）。

复杂度分析​

  • 时间复杂度：O(n²)。转置矩阵需遍历半个矩阵（O(n²/2)），反转每一行需遍历所有元素（O(n²/2)），总操作次数为O(n²)。
  • 空间复杂度：O(1)。所有操作均在原矩阵上进行，无需额外空间，完全满足“原地操作”要求。

边界情况验证​

  • n=1：矩阵只有一个元素，旋转后不变，操作有效。
  • n=2：如 [[1,2],[3,4]]，转置后为 [[1,3],[2,4]]，反转每一行后为 [[3,1],[4,2]]，符合顺时针旋转90度的结果。

这种“转置+反转”的方法是原地旋转矩阵的最优解，通过数学规律简化了操作步骤，避免了复杂的边界判断，效率更高且易于实现。