螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1：

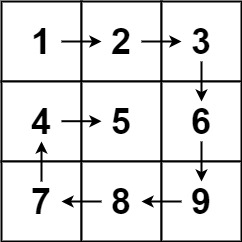
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5] 示例 2：

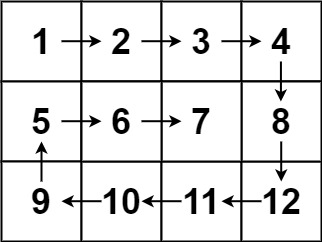
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

简单做法：配置顺时针四个方向依次执行xy轴加减规则来控制遍历方向，每次遍历结束记录边界，从第一行开始横向遍历，，遍历结束记录y start行数，再纵向遍历，记录x end列数，再逆横向遍历，记录y end行数，再逆纵向遍历，不得小于y start,结束遍历条件为横向和纵向都到达边界（和进阶做法一致）

进阶做法：通过逐层遍历的方式，从外层到内层依次处理每一圈元素。以下是具体的方法和实现：

方法思路

定义边界：使用四个变量 top、bottom、left、right 分别表示当前层的上、下、左、右边界。
遍历顺序：按照右 → 下 → 左 → 上的顺序遍历当前层的元素：
- 从左到右遍历顶部行（top）。
- 从上到下遍历右侧列（right）。
- 从右到左遍历底部行（bottom）。
- 从下到上遍历左侧列（left）。
收缩边界：每遍历完一层，将相应的边界向内收缩（top++、bottom--、left++、right--），继续处理内层。
终止条件：当边界交叉时（如 top > bottom 或 left > right），停止遍历。

代码实现

function spiralOrder(matrix) {
    if (matrix.length === 0) return [];
    
    const result = [];
    let top = 0, bottom = matrix.length - 1;
    let left = 0, right = matrix[0].length - 1;
    
    while (top <= bottom && left <= right) {
        // 从左到右遍历顶部行
        for (let j = left; j <= right; j++) {
            result.push(matrix[top][j]);
        }
        top++;
        
        // 从上到下遍历右侧列
        for (let i = top; i <= bottom; i++) {
            result.push(matrix[i][right]);
        }
        right--;
        
        // 检查是否还有行和列需要处理
        if (top > bottom || left > right) break;
        
        // 从右到左遍历底部行
        for (let j = right; j >= left; j--) {
            result.push(matrix[bottom][j]);
        }
        bottom--;
        
        // 从下到上遍历左侧列
        for (let i = bottom; i >= top; i--) {
            result.push(matrix[i][left]);
        }
        left++;
    }
    
    return result;
}

代码解释

初始化边界：top=0、bottom=m-1、left=0、right=n-1，表示矩阵的初始边界。
外层循环：通过 while 循环确保边界未交叉，继续处理当前层。
四个方向遍历：
- 顶部行：从 left 到 right，遍历后 top++（收缩上边界）。
- 右侧列：从 top 到 bottom，遍历后 right--（收缩右边界）。
- 底部行：从 right 到 left，遍历后 bottom--（收缩下边界）。
- 左侧列：从 bottom 到 top，遍历后 left++（收缩左边界）。
边界检查：每次收缩边界后，检查是否还有行和列需要处理（避免重复遍历）。

复杂度分析

时间复杂度：O(m×n)，每个元素仅被访问一次。
空间复杂度：O(1)，除结果数组外，仅使用常数级额外空间。

示例分析

以矩阵 matrix = [[1,2,3],[4,5,6],[7,8,9]] 为例：

初始边界：top=0、bottom=2、left=0、right=2。
第一轮遍历：
- 顶部行：[1,2,3]，top=1。
- 右侧列：[6,9]，right=1。
- 底部行：[8,7]，bottom=1。
- 左侧列：[4]，left=1。
第二轮遍历：
- 顶部行：[5]，top=2，left=2，right=0，bottom=0。
- 边界交叉，循环终止。

最终结果：[1,2,3,6,9,8,7,4,5]。

其他解法对比

模拟法：维护方向变量（右、下、左、上），遇到边界或已访问元素时转向。代码更复杂，但通用性强。
递归法：逐层递归处理，但可能导致栈溢出，且空间复杂度较高。

逐层遍历法是最直观且高效的解法，适用于各种矩阵形状（矩形、正方形）。

方法思路​

代码实现​

代码解释​

复杂度分析​

示例分析​

其他解法对比​